For the paper:

Brette R (2004) Dynamics of one-dimensional spiking neuron models. J
Math Biol 48:38-56

Abstract:

In this paper we make a rigorous mathematical analysis of
one-dimensional spiking neuron models in a unified framework. We find
that, under conditions satisfied in particular by the periodically and
aperiodically driven leaky integrator as well as some of its variants,
the spike map is increasing on its range, which leaves no room for
chaotic behavior. A rigorous expression of the Lyapunov exponent is
derived. Finally, we analyse the periodically driven perfect
integrator and show that the restriction of the phase map to its range
is always conjugated to a rotation, and we provide an explicit
expression of the invariant measure.

A brian simulator model is available at this web page:

http://briansimulator.org/docs/examples-frompapers_Brette_2004.html

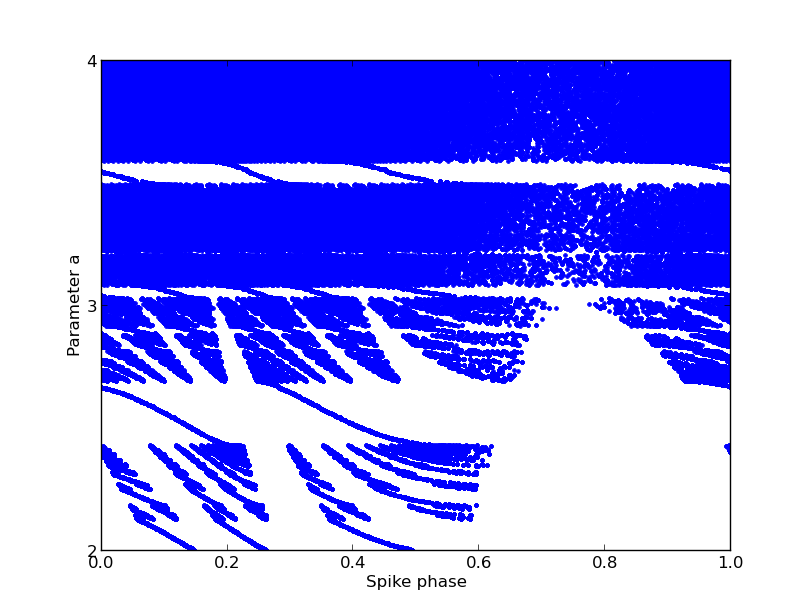
The simulation generates an image similar to Fig. 2A in the paper:



This simulation requires Brian which can be downloaded and installed
from the instructions available at http://www.briansimulator.org/

For support on installing and using Brian simulations there is a
support group at https://groups.google.com/group/briansupport.