Interface
The interface is a Python module named values.py located in the uppermost directory of the simulator code. It can be opened and its values can be changed for novel neural field simulations with any editor or integrated development environment.
The interface is text-based instead of graphical for four reasons.
- Cross-platform issues are non-existent with text.
- A GUI has overhead, particularly with event listeners, that slows simulations.
- Novel equations (kernels, firing rate functions, external inputs etc...) are easily integrated into simulations with Python coded text.
- People have different tastes. The editor that one most likes and is most comfortable with can be used with the interface; this is not so with a GUI.
The interface assigns values to dynamic neural field simulations of the type:
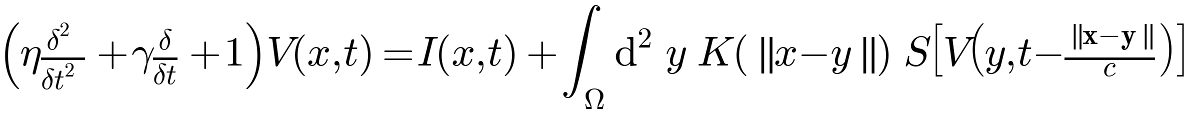
η is a second order derivative factor,
γ is a first order derivative factor,
V(x, t) is the mean potential of a neural population at position x and time t,
I(x, t) is the input from an external source at position x and time t,
Ω is the domain of integration of size l2,
K(x) is the synaptic connectivity kernel at spatial location x,
S(x) is the mean firing rate at position x and
c is the velocity (mm/s) of an action potential.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
'''Which data to show in the graph.
1 = show V, potential matrix updates
2 = show V0, potential matrix at time=0 (does not update V)
3 = show I, input matrix
4 = show K, kernel matrix '''
showData = 1
'''Temporal values.'''
endTime = -1 # sim duration (a float in secs or -1:infinity)
dt = 0.004 # temporal discretization (delta t in seconds)
'''Derivative factors.'''
gamma = 1.0 # first order
eta = 0.35 # second order
'''Axonal transmission speed value.'''
c = 20000 # mm/s
'''Field space values - applies to length and also width of square field.'''
l = 10.0 # field size
n = 256 # number of field discretized units
# This sets up the square field, x. Do not change the next 4 lines!!!! **********
import numpy as np
a,b= np.meshgrid(np.arange(-l/2.0,l/2.0,l/float(n)),np.arange(-l/2.0,l/2.0,l/float(n)))
x = np.sqrt(a**2+b**2)
# Do not change the previous 4 lines! *******************************************
'''This is the field voltage at time=0, V0.
You can delete/add/change variables but you must initialize a V0 = numpy array size n*n.'''
V0 = np.ones( (n,n) ) * 2.0 # our V at t=0 that will be used in the simulation
'''Noise applied to the voltage at t>=0, noiseVcont.
This variable is multiplied by a matrix of random numbers reset every epoc.
The noiseVcont variable can be None (for no continuous noise) or a numpy array of size n*n.'''
noiseVcont = None
'''This is data for the second order calculation, Uexcite.
You can delete/add/change variables but if eta is not 0.0,
you must initialize a Uexcite that is a numpy array of size n*n.
If eta (above) == 0.0, then Uexcite can be None, but this is not neccesary.'''
Uexcite = np.zeros((n,n)) # set Uexcite to zero
'''This is the input from external source, I.
You can delete/add/change variables but you must initialize an I that uses x.'''
I = 2.0 + np.exp(-x**2/0.25) / (0.25*np.pi)
'''This is the synaptic connectivity kernel, K.
You can delete/add/change variables but you must initialize a K that uses x.'''
phi_0 = 0*np.pi/3.0
phi_1 = 1*np.pi/3.0
phi_2 = 2*np.pi/3.0
k_c = 10*np.pi/l
dx = l/float(n)
K = 0.1*(np.cos(k_c*(a*np.cos(phi_0)+b*np.sin(phi_0))) + \
np.cos(k_c*(a*np.cos(phi_1)+b*np.sin(phi_1))) + \
np.cos(k_c*(a*np.cos(phi_2)+b*np.sin(phi_2))))* \
np.exp(-1 * x / 10.0) *dx *dx
'''This is the firing rate, S.
You can delete/add/change variables but you must keep the function name updateS and return the firing rate.'''
def updateS(V): # V is the passed in field voltage
S0 = 2.0 # maximum frequency
theta = 3.0 # firing threshold
alpha = 5.5 # steepness at the threshold
return S0 / (1.0 + np.exp(-1*alpha*(V-theta)))
'''Within this function you can update the external source, I, during the simulation.
You can delete/add/change variables but you must:
1. keep the function form: def updateI...
The parameter 'time' is the current simulation time in seconds which can be used for time-dependent shifts in I.
2. return your I value
'''
#def updateI(time):
# if time == 0.5: # Change I at a half second
# I = 2.0 + np.exp(-x**2/0.25) / (0.25*np.pi)
# return I
'''Within this function you can update the kernel, K, during the simulation.
You can delete/add/change variables but you must:
1. keep the function form: def updateK ...
The parameter 'time' is the current simulation time in seconds which can be used for time-dependent shifts in K.
2. 'return K' with no more text on the line at the end of the function.
'''
#def updateK(time):
# K += np.sin(time) / 10.0 # Add a sinusoid over time
# return K
Interface variables
var c
Axonal transmission speed in millimeters per second.
var dt
Temporal discretization in seconds.
var endTime
The simulation duration. This can be a float in seconds or -1 for infinity.
var eta
The second order derivative factor, η.
var gamma
The first order derivative factor, γ.
var I
The field voltage input from external sources.
If I is a single number, the value is applied homogeneously into every spatial location.
Otherwise, use x to input spatially heterogeneous values into the field, as shown in the example.
var K
The synaptic connectivity kernel.
Note that periodic boundary conditions are required for the integral which is solved by a Fourier series with discrete wave vectors.
The K matrix should therefore appear continuous when placed above and to the side of itself.
var l
The size of the field (mm) applicable to the length and the width.
var n
The number of field discretized units applicable to the length
and also the width of the square field.
This number
should be a power of 2, such as 28 to perform fast Fourier transforms.
var noiseVcont
Noise applied to the voltage every iteration of the simulation.
This variable is multiplied by a matrix of random numbers reset
every epoc.
This variable can be None (for no
continuous noise) or a numpy array of size n2.
var showData
Which data to show in the graph.
1 = show V, field potential updates
2 = show V0, field potential at time=0 (does not update V)
3 = show I, input matrix
4 = show K, kernel matrix
var Uexcite
A placeholder for the second order calculation that is used if eta is not 0.
var V0
The field voltage at the beginning of the simulation.
This can be a number, which the simulator applies homogeneously across the field, or a matrix of size
n2.
var x
This is the 2 dimensional field and should only be modified indirectly by changing other parameters, such as
l and
n.
Functions
def updateI(
time)
This is an optional function to be used only if the input from an external source is changed during the simulation.
The time parameter is in seconds and can be used to change I at a given time.
You can modify the contents of this function.
However, you must keep the function declaration (def updateI(time): ...
and return an I value).
def updateI(time):
if time == 0.5: # Change I at a half second
I = 2.0 + np.exp(-x**2/0.25) / (0.25*np.pi)
return Idef updateK(
time)
This is an optional function to be used only if the synaptic connectivity kernel is changed during the simulation.
The time parameter is in seconds and can be used to change K at a given time.
Note: if you implement this function, K must has a periodic boundary condition
(see K above).
You can modify the contents of this function.
However, you must keep the function declaration (def updateK(time): ... and return a K value).
def updateK(time):
K += np.sin(time) / 2.0 # Add a sinusoid over time
return Kdef updateS(
V)
This function is necessary for the firing rate within the neural field.
The V parameter is the field voltage matrix.
You can modify the contents of this function.
However, you must...
- keep the function declaration (
def updateS(V):... and return a matrix representing the firing rate) - have the returned matrix appear continuous when placed above and to the side of itself,
because
Shas a periodic boundary condition. A sigmoidal function, such as in the example, is a good choice for the firing rate.
def updateS(V):
S0 = 2.0 # maximum frequency
theta = 3.0 # firing threshold
alpha = 5.5 # steepness at the threshold
return S0 / (1.0 + np.exp(-1*alpha*(V-theta)))