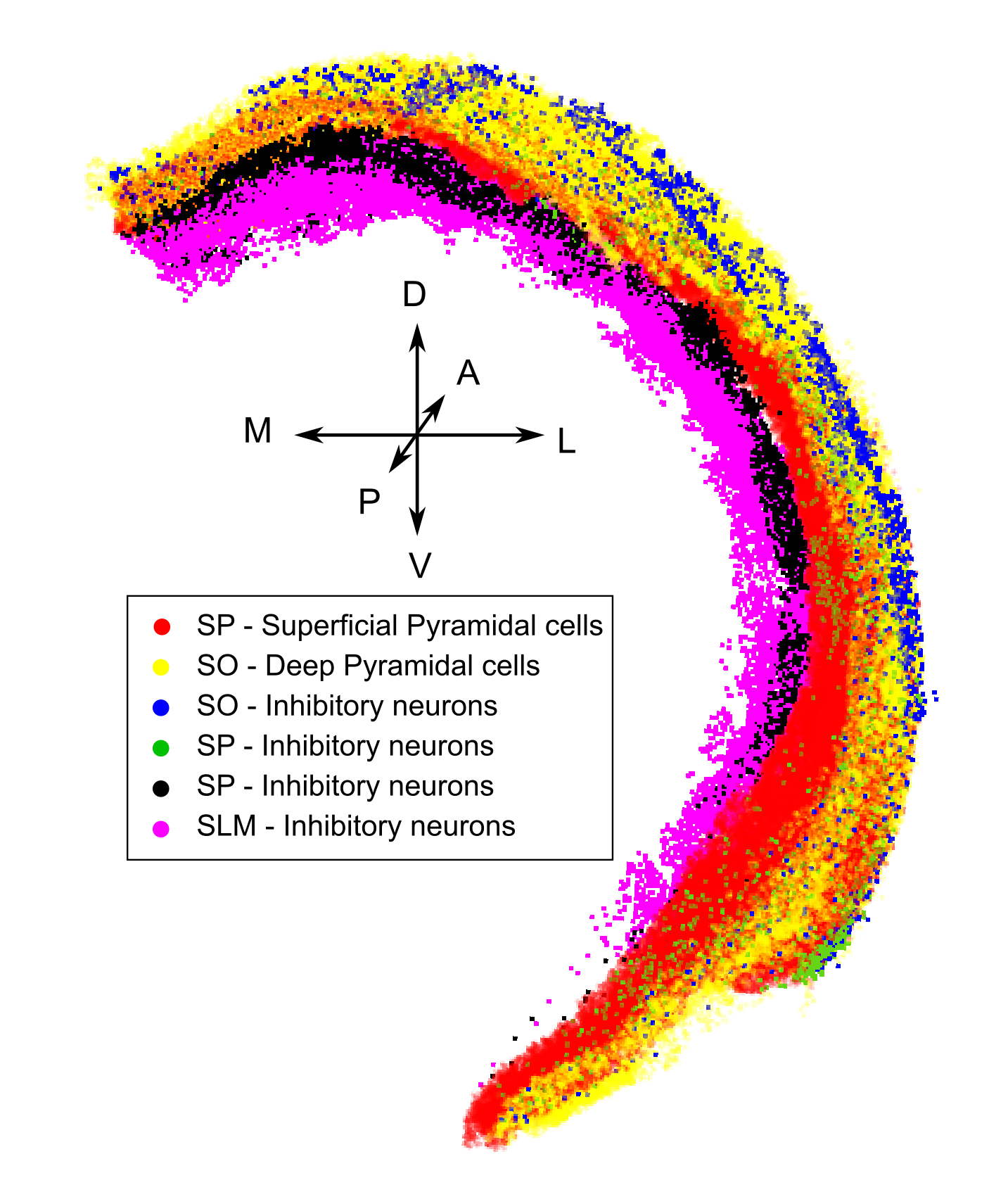
Fig 1. Excitatory and inhibitory cell placements according to the CA1 region layer subdivision provided by the Blue Brain cell Atlas.
create_pyramidal_morphology_2.ipynb

Fig 1. Excitatory and inhibitory cell placements according to the CA1 region layer subdivision provided by the Blue Brain cell Atlas.
In our approach, the rule to generate a connection between any two neurons was implemented assuming that neuronal classes are characterized by specific morphological properties.
These properties have been modeled as combinations of ellipsoids and cones mimicking the cross-section volume of pre-synaptic axons and post-synaptic dendrites .
In general, the probability cloud eigenvalue parametrization depended on the relative distances between each cell soma location and its CA1 targeting subregion while the probability cloud eigenvectors parametrization depended on the relative orientations between each soma location and its CA1 targeting subregion.
All cells were associated with their relative distances from CA3 and from Subiculum, in order to consider the experimentally observed preferential orientation of PC axons along the direction of the minimum distance between CA3 and Subiculum.
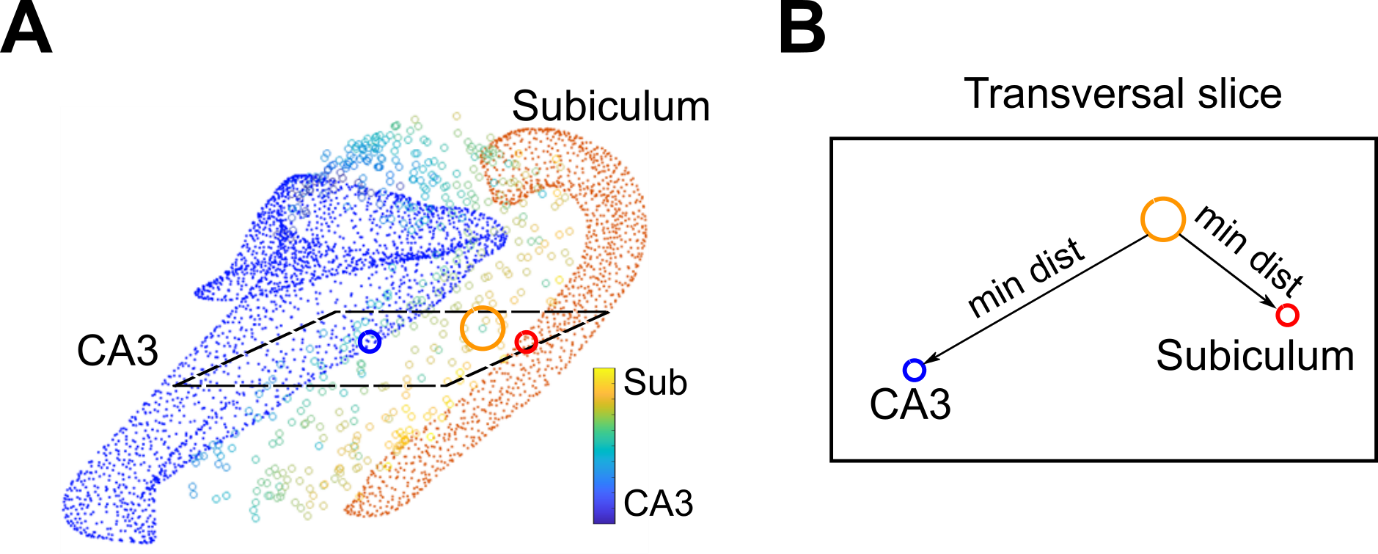
Fig 2. “Positional-Morpho-Anatomical” modelling. CA1 PC cells are indicated by orange circle.
Assuming that any quadratic function $f (x_1, . . . , x_n)$ can be written in the form $ X ^\mathsf{T} Q X $, where $ Q$ is a symmetric matrix ( $ Q = Q^\mathsf{T} $ ), given a system of eigenvectors that diagonalize the symmetric matrix, any ellipsoid can be described as a volume oriented in the direction set by the eigenvectors and elongated along the semi-axis as set by the eigenvalues.
Considering an orthonormal system of eigenvectors $ \mathbf{v_1, v_2, v_3}$ associated, respectively, with the eigenvalues $ \lambda_1, \lambda_2, \lambda_3$ of a $3 \times 3$ symmetric positive matrix $M$. If
$$
V = [ \mathbf{v_1, v_2, v_3} ] ,
$$
Then
$$
V^\mathsf{T} M V = \Bigg[ \begin{matrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_2 & 0 \\
0 & 0 & \lambda_3 \\
\end{matrix} \Bigg] = D \,[\lambda_1, \lambda_2, \lambda_3 ]
$$
So we built the symmetric matrix ($Q$) starting from an arbitrary base of orthonormal vectors $ \mathbf{u_1, u_2, u_3}$ (ellipsoid orientation vectors) forming the matrix $U$ and diagonal matrix $D$ of arbitrary eigenvalues (semiaxis lengths) $ Q = U D U^\mathsf{T} $.
The probability cloud associated with the ellipsoid was then modelled as scattered tridimensional points following the canonical parametric equations:
$$ \begin{align} x &= \lambda_1 \cos \theta \sin \phi, \\ y &= \lambda_2 \cos \theta \sin \phi, \\ z &= \lambda_3 \cos \phi \\ \end{align} $$where $ \; \; 0 \leq \theta \leq 2 \pi \; \; and \; \; −\pi \leq \phi \leq 0 $.
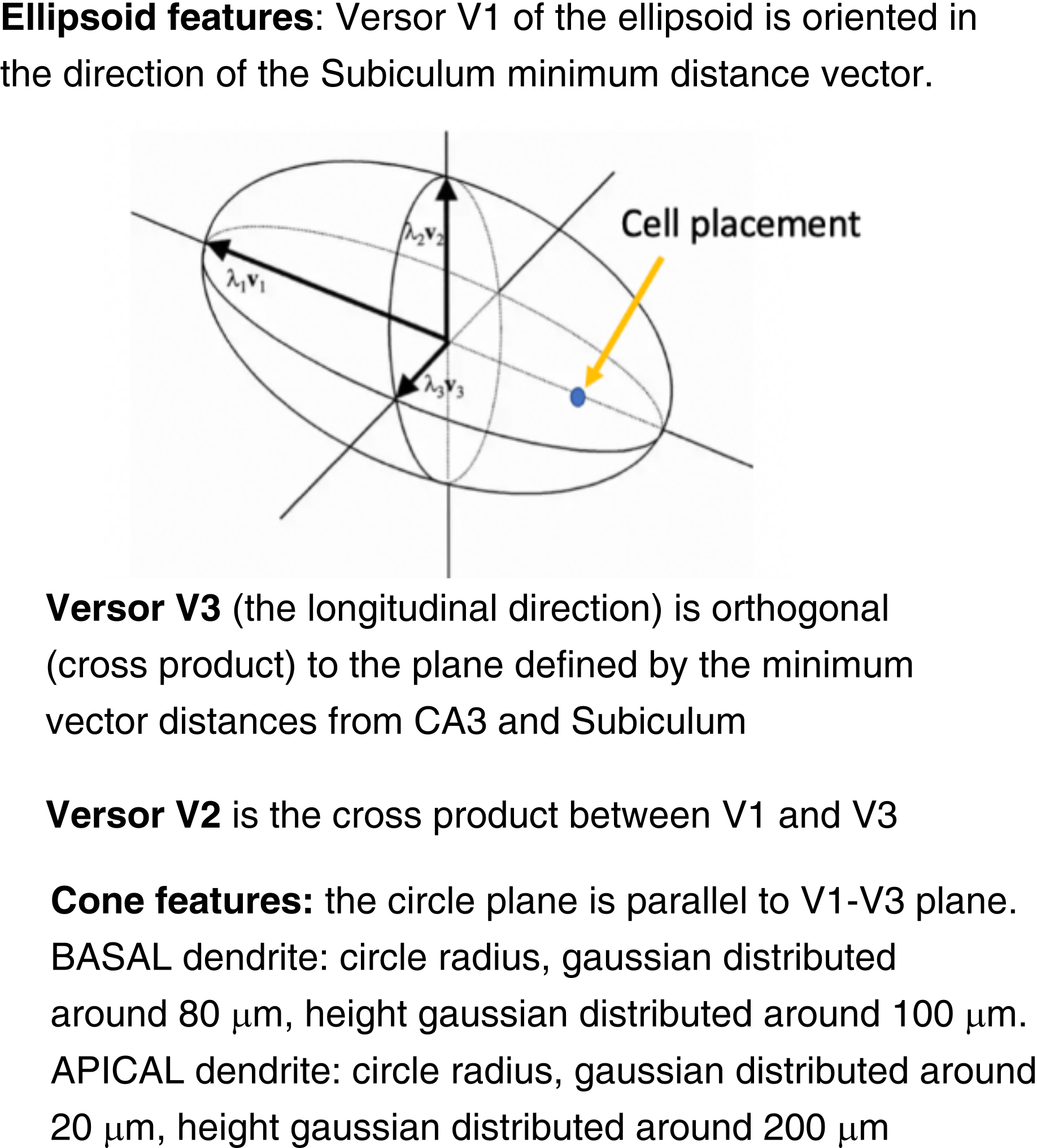
Pyramidal dendrites are modeled as conic probability clouds. u and v are two orthogonal vectors that lie in the plane of the circle forming the basis of the cone. To build a cone between point $ O $ (apex) and base center point ($ P $) with a given radius $ R $ we determined the norm of the cone base plane, which is given by $ d = P - O $.
The probability cloud associated with the cone was then modelled as scattered tridimensional points following the general parametric equation:
$$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{pmatrix} O_x + \frac{h}{H} dx \\ O_y + \frac{h}{H} dy \\ O_z + \frac{h}{H} dz \end{pmatrix} + \begin{pmatrix} R \cdot \frac{h}{H} \cdot \cos \theta \cdot u_x \\ R \cdot \frac{h}{H} \cdot \cos \theta \cdot u_y \\ R \cdot \frac{h}{H} \cdot \cos \theta \cdot u_z \end{pmatrix} + \begin{pmatrix} R \cdot \frac{h}{H} \cdot \sin \theta \cdot v_x \\ R \cdot \frac{h}{H} \cdot \sin \theta \cdot v_y \\ R \cdot \frac{h}{H} \cdot \sin \theta \cdot v_z \end{pmatrix} $$with $\quad 0 \leq h \leq H, \quad 0 \leq \theta \leq 2 \pi $
where $ H = |P - O| = d $.
import numpy as np
import pandas as pd
import scipy.io
from scipy.spatial import ConvexHull
from itertools import product
import matplotlib.pyplot as plt
from matplotlib import cm
PyrS_features = scipy.io.loadmat('PyrS_features.mat')
PyrS_features_df = pd.DataFrame( PyrS_features['PyrS_features'])
ColumnNames = ['PlacementPyr_x', 'PlacementPyr_y', 'PlacementPyr_z',
'MinDistCA3', 'MinDistCA3_x', 'MinDistCA3_y', 'MinDistCA3_z',
'MinDistSub', 'MinDistSub_x', 'MinDistSub_y', 'MinDistSub_z',
'eigenv_ellips_l1', 'eigenv_ellips_l2', 'eigenv_ellips_l3',
'H_BasalDend', 'r_BasalDend','H_ApicalDend', 'r_ApicalDend', 'nn',
'MinDistOriens','MinDistOriens_x','MinDistOriens_y','MinDistOriens_z',
'MinDistLacun','MinDistLacun_x','MinDistLacun_y','MinDistLacun_z']
PyrS_features_df.columns = ColumnNames
PyrS_features_df
| PlacementPyr_x | PlacementPyr_y | PlacementPyr_z | MinDistCA3 | MinDistCA3_x | MinDistCA3_y | MinDistCA3_z | MinDistSub | MinDistSub_x | MinDistSub_y | ... | r_ApicalDend | nn | MinDistOriens | MinDistOriens_x | MinDistOriens_y | MinDistOriens_z | MinDistLacun | MinDistLacun_x | MinDistLacun_y | MinDistLacun_z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8125.370117 | 2469.269775 | 9085.161133 | 600.477478 | 7744.009766 | 2885.100098 | 8879.679688 | 959.296570 | 8988.040039 | 2366.489990 | ... | 75.562119 | 1.0 | 44.070309 | 8102.819824 | 2440.929932 | 9110.271484 | 268.089783 | 8122.830078 | 2677.699951 | 8916.571289 |
| 1 | 8176.560059 | 3510.365967 | 9620.210938 | 376.325958 | 7882.220215 | 3629.330078 | 9418.139648 | 1015.934021 | 9184.879883 | 3528.199951 | ... | 72.826775 | 2.0 | 108.608330 | 8128.389648 | 3473.450928 | 9710.281250 | 308.827515 | 8224.769531 | 3671.210938 | 9361.021484 |
| 2 | 7935.819824 | 5826.859863 | 8160.361328 | 37.691891 | 7916.029785 | 5796.759766 | 8149.270020 | 1309.069458 | 9080.230469 | 5367.250000 | ... | 90.401756 | 3.0 | 101.279541 | 7905.229980 | 5898.060059 | 8225.571289 | 51.631149 | 7980.679688 | 5810.830078 | 8140.451172 |
| 3 | 8230.169922 | 2692.069824 | 9283.851562 | 608.663940 | 7816.259766 | 3013.169922 | 8973.940430 | 937.358215 | 9137.700195 | 2683.639893 | ... | 58.591160 | 4.0 | 72.143684 | 8245.179688 | 2652.079834 | 9341.991211 | 211.220276 | 8314.849609 | 2787.929932 | 9115.761719 |
| 4 | 8718.200195 | 4007.935791 | 9805.201172 | 800.595398 | 8240.089844 | 3964.889893 | 9164.490234 | 489.271667 | 9188.759766 | 4043.209961 | ... | 65.722137 | 5.0 | 78.015656 | 8762.959961 | 3949.673828 | 9831.441406 | 308.917267 | 8701.339844 | 4021.460938 | 9497.041016 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 216430 | 8022.179688 | 2303.029785 | 8942.380859 | 609.587769 | 7711.689941 | 2799.010010 | 8771.509766 | 978.513672 | 8861.049805 | 2161.629883 | ... | 54.149960 | 216431.0 | 49.564491 | 8041.060059 | 2308.499756 | 8987.880859 | 272.917908 | 8151.359863 | 2368.969971 | 8711.191406 |
| 216431 | 8197.729492 | 5001.349609 | 9580.071289 | 540.179443 | 7890.080078 | 4773.049805 | 9199.250000 | 937.382385 | 9113.049805 | 5022.910156 | ... | 73.821106 | 216432.0 | 63.861050 | 8155.500000 | 4957.020020 | 9561.911133 | 401.460388 | 8352.639648 | 4764.562988 | 9295.281250 |
| 216432 | 8316.330078 | 3736.258789 | 9763.931641 | 524.106201 | 7952.270020 | 3733.139893 | 9386.919922 | 884.767029 | 9190.419922 | 3823.790039 | ... | 73.559975 | 216433.0 | 107.298393 | 8282.729492 | 3687.611816 | 9853.471680 | 258.790009 | 8321.149414 | 3801.478271 | 9513.541016 |
| 216433 | 8199.200195 | 2605.719971 | 9225.611328 | 613.186035 | 7816.259766 | 3013.169922 | 8973.940430 | 949.058411 | 9106.450195 | 2624.780029 | ... | 63.066402 | 216434.0 | 80.917030 | 8231.530273 | 2564.829834 | 9287.500977 | 234.244354 | 8334.459961 | 2703.499756 | 9061.250977 |
| 216434 | 6990.308105 | 1737.569824 | 7572.471191 | 470.250702 | 6677.490234 | 2086.320068 | 7613.140137 | 1175.725464 | 7978.209961 | 1884.729980 | ... | 52.314598 | 216435.0 | 52.514091 | 7010.776855 | 1691.729858 | 7557.061523 | 241.867889 | 7150.609863 | 1907.689819 | 7510.321289 |
216435 rows × 27 columns
'''
This script creates morphologies of superficial pyramidal cells.
Axons are modelled as ellipsoids and dendrites as probability clouds distributed in a conic volume.
They are created by the DataFrame containing all the necessary features.
It returns a dictionary with axonal and dendritic probability clouds for each pyramidal cell.
'''
rP = np.size(PyrS_features_df,0) # number of pyramidal cells
rP = 100 # number of simulated cells
PyrS_M = {} ; Pyrtemp = {}
for w in range(rP):
print('pyramidal cell n: ',w+1)
PyrS_M[w] = {}
#### CREATION OF FIRST ELLIPSOID ####
#creation of the eigenvectors for ellipsoid projecting towards stratum oriens
Dx = 10
Dy = 10
Dz = ( 0.5 * PyrS_features_df['MinDistOriens'][w] ) + 20
N = 8 # number of concentric ellipes defining ellipsoid
D = np.zeros((3,3))
D[0,0] = Dx**2; D[1,1] = Dy**2; D[2,2] = Dz**2;
p1 = PyrS_features_df.loc[w, ['PlacementPyr_x','PlacementPyr_y','PlacementPyr_z'] ].values
por = PyrS_features_df.loc[w, ['MinDistOriens_x','MinDistOriens_y','MinDistOriens_z'] ].values
plm = PyrS_features_df.loc[w, ['MinDistLacun_x','MinDistLacun_y','MinDistLacun_z'] ].values
# create eigenvectors: semi-axes of the first ellipsoid (vx, vy, vz)
vz = por - plm # eigenvector vz
vz = vz / np.linalg.norm(vz,2)
vor = por - p1 # vector connecting pyramidal to oriens
vor = vor / np.linalg.norm(vor,2)
vnorm = np.cross(vz,vor) # create vector orthogonal to plane defined by vz e vor
vnorm = vnorm / np.linalg.norm(vnorm,2)
vy = vnorm # eigenvector vy
vx = np.cross(vz,vy) # eigenvector vx orthogonal to plane z,y
V = np.stack((vx, vy, vz), axis=1)
Q = np.dot(V,np.dot(D,V.T))
(d,V) = np.linalg.eig(Q)
s = np.argsort(d)
D = np.sort(d)
V = V[:,s]; D = np.real(D)
uv = np.arange(-1,1+2/(N-1),2/(N-1))
u,v = np.meshgrid( uv *np.pi/2, uv *np.pi )
# x,y,z for definition of concentric ellipses
x = D[0]**.5 * np.cos(u) * np.cos(v)
y = D[1]**.5 * np.cos(u) * np.sin(v)
z = D[2]**.5 * np.sin(u)
# shift vector to move ellipsoid center in a different point than pyramidal cell placement
Vshift = ( PyrS_features_df['MinDistOriens'][w] + 20 ) * vz;
# temporary coordinates of ellipsoid center
qtemp = np.zeros(3)
qtemp[0] = p1[0] + Vshift[0]
qtemp[1] = p1[1] + Vshift[1]
qtemp[2] = p1[2] + Vshift[2]
xx = np.zeros((N,N)); yy = np.zeros((N,N)); zz = np.zeros((N,N));
for k,j in product( range(len(x)), range(len(x)) ):
point = - np.dot( V, np.vstack([x[k,j], y[k,j], z[k,j]]) )
xx[k,j] = point[0] + qtemp[0]
yy[k,j] = point[1] + qtemp[1]
zz[k,j] = point[2] + qtemp[2]
# allocate in (axon1) the coordinates of first axonal cloud
P = np.hstack([ np.reshape(xx,(-1,1)) , np.reshape(yy,(-1,1)) , np.reshape(zz,(-1,1)) ])
P = np.hstack([ P , np.ones((np.size(P,0),1)) * w ])
PyrS_M[w]['axon1'] = P
#### CREATION OF SECOND ELLIPSOID ####
# axon2 is created with the same procedure as axon1 with different eigenvalues and eigenvectors
Dx = PyrS_features_df['eigenv_ellips_l1'][w]
Dy = PyrS_features_df['eigenv_ellips_l2'][w]
Dz = PyrS_features_df['eigenv_ellips_l3'][w]
N = 8 # number of concentric ellipes defining second ellipsoid
D = np.zeros((3,3))
D[0,0] = Dx**2; D[1,1] = Dy**2; D[2,2] = Dz**2;
Vshift2 = 2*Dz*vz # second shift from pyramidal cell placement
p1 = PyrS_features_df.loc[w, ['PlacementPyr_x','PlacementPyr_y','PlacementPyr_z']].values + Vshift2
pCA3 = PyrS_features_df.loc[w, ['MinDistCA3_x', 'MinDistCA3_y', 'MinDistCA3_z']].values
psub = PyrS_features_df.loc[w, ['MinDistSub_x', 'MinDistSub_y', 'MinDistSub_z']].values
vx = psub - p1
vz = vz / np.linalg.norm(vz,2)
vx = vx / np.linalg.norm(vx,2)
vsub = p1 - pCA3
vsub = vsub / np.linalg.norm(vsub,2)
vnorm = np.cross(vx,vsub)
vnorm = vnorm / np.linalg.norm(vnorm,2)
vy = vnorm
vz = np.cross(vx,vy)
V[:,0] = vx; V[:,1] = vy; V[:,2] = vz
Q = np.dot(V,np.dot(D,V.T))
(d,V) = np.linalg.eig(Q)
s = np.argsort(d)
D = np.sort(d)
V = V[:,s]
uv = np.arange(-1,1+2/(N-1),2/(N-1))
u,v = np.meshgrid( uv *np.pi/2, uv *np.pi )
x = D[0]**.5 * np.cos(u) * np.cos(v)
y = D[1]**.5 * np.cos(u) * np.sin(v)
z = D[2]**.5 * np.sin(u)
Vshift3 = 0.75 * Dx * vx # third shift
qtemp = np.zeros(3)
qtemp[0] = p1[0] + Vshift3[0];
qtemp[1] = p1[1] + Vshift3[1];
qtemp[2] = p1[2] + Vshift3[2];
xx = np.zeros((N,N)); yy = np.zeros((N,N)); zz = np.zeros((N,N));
for k,j in product( range(len(x)),range(len(x)) ):
point = - np.dot( V, np.vstack([x[k,j], y[k,j], z[k,j]]) )
xx[k,j] = point[0] + qtemp[0]
yy[k,j] = point[1] + qtemp[1]
zz[k,j] = point[2] + qtemp[2]
# allocate in (axon2) the coordinates of second axonal cloud
P = np.hstack([ np.reshape(xx,(-1,1)), np.reshape(yy,(-1,1)), np.reshape(zz,(-1,1)) ])
P = np.hstack([ P , np.ones((np.size(P,0),1))*w ])
PyrS_M[w]['axon2'] = P
#### CREATE COORDINATES OF BASAL AND APICAL DENDRITES ####
'''
While ellipsoid is build through (empty) concentric ellipses, dendrites
are made of a collection of points randomly distributed to form a cone
'''
# u and v are parallel to the axon travelling towards subiculum
u = vx
v = vy
vlm = plm - p1
vlm = vlm / np.linalg.norm(vlm,2)
Dlm = PyrS_features_df['MinDistLacun'][w]
# cone1 is the BASAL one (the upper, shorter and larger, inserted in stratum oriens)
# cone2 is the APICAL one (the lower, longer and narrowe, inserted in stratum radiatum)
H1 = PyrS_features_df['H_BasalDend'][w]
H2 = PyrS_features_df['H_ApicalDend'][w]
Vcone1 = H1 * vlm
Vcone2 = H2 * vlm
O = PyrS_features_df.loc[w, ['PlacementPyr_x','PlacementPyr_y','PlacementPyr_z']].values #cone origin
P1 = np.zeros(3); P2 = np.zeros(3);
P1[0] = O[0] + Vcone1[0] # origin of cone1 circular base
P1[1] = O[1] + Vcone1[1]
P1[2] = O[2] + Vcone1[2]
P2[0] = O[0] - Vcone2[0] # origin of cone2 circular base
P2[1] = O[1] - Vcone2[1]
P2[2] = O[2] - Vcone2[2]
d1 = np.hstack([O[0] - P1[0] , O[1] - P1[1] , O[2] - P1[2] ])
d2 = np.hstack([O[0] - P2[0] , O[1] - P2[1] , O[2] - P2[2] ])
N = 100 # number of points for the description of cross section (volume)
theta = np.random.rand(N,1) * 2 * np.pi
h1 = np.random.rand(N,1) * H1
h2 = np.random.rand(N,1) * H2
R1 = np.random.rand(N,1) * PyrS_features_df['r_BasalDend'][w]
R2 = np.random.rand(N,1) * PyrS_features_df['r_ApicalDend'][w]
x1 = O[0] + (h1/H1)*d1[0] + R1*(h1/H1)*np.cos(theta)*u[0] + R1*(h1/H1)*np.sin(theta)*v[0]
y1 = O[1] + (h1/H1)*d1[1] + R1*(h1/H1)*np.cos(theta)*u[1] + R1*(h1/H1)*np.sin(theta)*v[1]
z1 = O[2] + (h1/H1)*d1[2] + R1*(h1/H1)*np.cos(theta)*u[2] + R1*(h1/H1)*np.sin(theta)*v[2]
x2 = O[0] + (h2/H2)*d2[0] + R2*(h2/H2)*np.cos(theta)*u[0] + R2*(h2/H2)*np.sin(theta)*v[0]
y2 = O[1] + (h2/H2)*d2[1] + R2*(h2/H2)*np.cos(theta)*u[1] + R2*(h2/H2)*np.sin(theta)*v[1]
z2 = O[2] + (h2/H2)*d2[2] + R2*(h2/H2)*np.cos(theta)*u[2] + R2*(h2/H2)*np.sin(theta)*v[2]
# allocate in (dendrite1) and (dendrite2) the coordinates of basal and apical dendrites.
# allocate in (DENDRITES) all the dendrites
Pyrtemp[w] = {}
Pyrtemp[w]['dendrite1'] = np.hstack([ x1 , y1 , z1, np.ones((len(x1),1))*w ])
Pyrtemp[w]['dendrite2'] = np.hstack([ x2 , y2 , z2, np.ones((len(x2),1))*w ])
PyrS_M[w]['DENDRITES'] = np.vstack([ Pyrtemp[w]['dendrite1'] , Pyrtemp[w]['dendrite2'] ])
PyrS_M[w]['dendrite1'] = Pyrtemp[w]['dendrite1']
PyrS_M[w]['dendrite2'] = Pyrtemp[w]['dendrite2']
# convex hull or convex envelope of a shape is the smallest convex set that contains it
PyrS_M[w]['AXONShull1'] = ConvexHull( PyrS_M[w]['axon1'][:,0:3] )
PyrS_M[w]['AXONShull2'] = ConvexHull( PyrS_M[w]['axon2'][:,0:3] )
pyramidal cell n: 1 pyramidal cell n: 2 pyramidal cell n: 3 pyramidal cell n: 4 pyramidal cell n: 5 pyramidal cell n: 6 pyramidal cell n: 7 pyramidal cell n: 8 pyramidal cell n: 9 pyramidal cell n: 10 pyramidal cell n: 11 pyramidal cell n: 12 pyramidal cell n: 13 pyramidal cell n: 14 pyramidal cell n: 15 pyramidal cell n: 16 pyramidal cell n: 17 pyramidal cell n: 18 pyramidal cell n: 19 pyramidal cell n: 20 pyramidal cell n: 21 pyramidal cell n: 22 pyramidal cell n: 23 pyramidal cell n: 24 pyramidal cell n: 25 pyramidal cell n: 26 pyramidal cell n: 27 pyramidal cell n: 28 pyramidal cell n: 29 pyramidal cell n: 30 pyramidal cell n: 31 pyramidal cell n: 32 pyramidal cell n: 33 pyramidal cell n: 34 pyramidal cell n: 35 pyramidal cell n: 36 pyramidal cell n: 37 pyramidal cell n: 38 pyramidal cell n: 39 pyramidal cell n: 40 pyramidal cell n: 41 pyramidal cell n: 42 pyramidal cell n: 43 pyramidal cell n: 44 pyramidal cell n: 45 pyramidal cell n: 46 pyramidal cell n: 47 pyramidal cell n: 48 pyramidal cell n: 49 pyramidal cell n: 50 pyramidal cell n: 51 pyramidal cell n: 52 pyramidal cell n: 53 pyramidal cell n: 54 pyramidal cell n: 55 pyramidal cell n: 56 pyramidal cell n: 57 pyramidal cell n: 58 pyramidal cell n: 59 pyramidal cell n: 60 pyramidal cell n: 61 pyramidal cell n: 62 pyramidal cell n: 63 pyramidal cell n: 64 pyramidal cell n: 65 pyramidal cell n: 66 pyramidal cell n: 67 pyramidal cell n: 68 pyramidal cell n: 69 pyramidal cell n: 70 pyramidal cell n: 71 pyramidal cell n: 72 pyramidal cell n: 73 pyramidal cell n: 74 pyramidal cell n: 75 pyramidal cell n: 76 pyramidal cell n: 77 pyramidal cell n: 78 pyramidal cell n: 79 pyramidal cell n: 80 pyramidal cell n: 81 pyramidal cell n: 82 pyramidal cell n: 83 pyramidal cell n: 84 pyramidal cell n: 85 pyramidal cell n: 86 pyramidal cell n: 87 pyramidal cell n: 88 pyramidal cell n: 89 pyramidal cell n: 90 pyramidal cell n: 91 pyramidal cell n: 92 pyramidal cell n: 93 pyramidal cell n: 94 pyramidal cell n: 95 pyramidal cell n: 96 pyramidal cell n: 97 pyramidal cell n: 98 pyramidal cell n: 99 pyramidal cell n: 100
## PLOT SUPERFICIAL PYRAMIDAL MORPHOLOGY ##
%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6,6))
ax = Axes3D(fig)
col = np.round(np.linspace(0,255,rP))
cmap = cm.jet
for w in range(rP):
ptsd = PyrS_M[w]['dendrite1']
ax.scatter(ptsd[:,0], ptsd[:,1], ptsd[:,2], '.', color=[0, .8, 0], s=1.8 )
ptsd2 = PyrS_M[w]['dendrite2']
ax.scatter(ptsd2[:,0], ptsd2[:,1], ptsd2[:,2], '.', color=[0, .2, 1], s=1.8 )
pts = PyrS_M[w]['axon1']
ax.plot(pts[:,0], pts[:,1], pts[:,2], '.', c=[.9, 0, .8] , markersize=2 )
pts2 = PyrS_M[w]['axon2']
ax.plot(pts2[:,0], pts2[:,1], pts2[:,2], '.', c=[.9, 0, .8], markersize=2 )
fig.suptitle('Hippocampus (superficial) pyramidal cells morphology')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.grid(False)
plt.show()
import numpy as np
import pandas as pd
import scipy.io
from scipy.spatial import ConvexHull
from itertools import product
import matplotlib.pyplot as plt
from matplotlib import cm
PyrD_features = scipy.io.loadmat('PyrD_features.mat')
PyrD_features_df = pd.DataFrame( PyrD_features['PyrD_features'])
ColumnNames = ['PlacementPyr_x', 'PlacementPyr_y', 'PlacementPyr_z',
'MinDistCA3', 'MinDistCA3_x', 'MinDistCA3_y', 'MinDistCA3_z',
'MinDistSub', 'MinDistSub_x', 'MinDistSub_y', 'MinDistSub_z',
'eigenv_ellips_l1', 'eigenv_ellips_l2', 'eigenv_ellips_l3',
'H_BasalDend', 'r_BasalDend','H_ApicalDend', 'r_ApicalDend', 'nn',
'MinDistOriens','MinDistOriens_x','MinDistOriens_y','MinDistOriens_z',
'MinDistLacun','MinDistLacun_x','MinDistLacun_y','MinDistLacun_z']
PyrD_features_df.columns = ColumnNames
PyrD_features_df
| PlacementPyr_x | PlacementPyr_y | PlacementPyr_z | MinDistCA3 | MinDistCA3_x | MinDistCA3_y | MinDistCA3_z | MinDistSub | MinDistSub_x | MinDistSub_y | ... | r_ApicalDend | nn | MinDistOriens | MinDistOriens_x | MinDistOriens_y | MinDistOriens_z | MinDistLacun | MinDistLacun_x | MinDistLacun_y | MinDistLacun_z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7392.106934 | 1747.999878 | 6732.710449 | 890.852295 | 7059.520020 | 2480.439941 | 7115.509766 | 481.840271 | 7805.290039 | 1948.609985 | ... | 75.934700 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 234.771942 | 7299.580078 | 1944.149902 | 6822.609375 |
| 1 | 7621.520020 | 1876.859863 | 8444.201172 | 628.380432 | 7357.609863 | 2436.050049 | 8332.309570 | 1056.485596 | 8534.780273 | 1838.369995 | ... | 71.809219 | 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 327.164154 | 7824.839844 | 2055.999756 | 8260.880859 |
| 2 | 8242.309570 | 4284.031738 | 9922.581055 | 604.455139 | 7884.509766 | 4205.689941 | 9441.740234 | 976.706604 | 9181.580078 | 4373.419922 | ... | 79.149597 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 449.711182 | 8482.290039 | 4196.378906 | 9552.491211 |
| 3 | 7902.299805 | 1866.799805 | 8285.681641 | 760.362732 | 7498.049805 | 2510.729980 | 8295.030273 | 733.929565 | 8534.780273 | 1838.369995 | ... | 65.585480 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 158.995499 | 7922.120117 | 2017.859863 | 8240.210938 |
| 4 | 8585.219727 | 2023.969849 | 8492.821289 | 944.984985 | 8081.180176 | 2794.449951 | 8279.980469 | 253.315735 | 8810.830078 | 2034.680054 | ... | 86.468346 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 252.800308 | 8631.629883 | 2248.109863 | 8385.511719 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 45403 | 8710.139648 | 3970.956787 | 9976.451172 | 927.806396 | 8133.100098 | 3930.250000 | 9251.059570 | 563.599426 | 9205.879883 | 3958.399902 | ... | 67.252625 | 45404.0 | 0.0 | 0.0 | 0.0 | 0.0 | 479.555908 | 8534.519531 | 4050.527832 | 9537.361328 |
| 45404 | 8492.479492 | 1886.529907 | 8391.851562 | 993.687744 | 8043.640137 | 2757.699951 | 8227.469727 | 284.303741 | 8700.129883 | 1938.589966 | ... | 69.881683 | 45405.0 | 0.0 | 0.0 | 0.0 | 0.0 | 329.694336 | 8392.959961 | 2137.069824 | 8202.051758 |
| 45405 | 7346.531738 | 1707.459839 | 6708.384277 | 919.362610 | 6983.200195 | 2498.370117 | 7004.490234 | 532.282715 | 7805.290039 | 1948.609985 | ... | 73.362648 | 45406.0 | 0.0 | 0.0 | 0.0 | 0.0 | 266.971924 | 7299.580078 | 1944.149902 | 6822.609375 |
| 45406 | 6590.809570 | 1857.409912 | 6773.599121 | 324.349274 | 6431.700195 | 2124.780029 | 6865.250000 | 1213.702148 | 7727.000000 | 2113.169922 | ... | 68.168320 | 45407.0 | 0.0 | 0.0 | 0.0 | 0.0 | 244.541473 | 6804.740723 | 1888.679810 | 6659.335449 |
| 45407 | 8286.349609 | 1671.939819 | 8027.061523 | 1049.507446 | 7832.270020 | 2617.790039 | 8052.459961 | 305.399933 | 8509.259766 | 1774.050049 | ... | 67.491074 | 45408.0 | 0.0 | 0.0 | 0.0 | 0.0 | 327.380371 | 8327.570312 | 1993.229858 | 8074.511230 |
45408 rows × 27 columns
'''
This function creates morphologies of deep pyramidal cells.
Axons are modelled as ellipsoids and dendrites as probability clouds distributed in a conic volume.
They are created by the DataFrame containing all the necessary features
It returns a dictionary with axonal and dendritic probability clouds for each pyramidal cell
'''
rP = np.size(PyrD_features_df,0) # number of pyramidal cells
rP = 100 # number of simulated cells
PyrD_M = {} ; Pyrtemp = {}
for w in range(rP):
print('pyramidal cell n: ',w+1)
PyrD_M[w] = {}
#### CREATION OF FIRST ELLIPSOID ####
#creation of the eigenvectors for ellipsoid projecting towards stratum oriens
Dx = PyrD_features_df['eigenv_ellips_l1'][w]
Dy = PyrD_features_df['eigenv_ellips_l2'][w]
Dz = PyrD_features_df['eigenv_ellips_l3'][w]
N = 8 # number of concentric ellipes defining ellipsoid
D = np.zeros((3,3))
D[0,0] = Dx**2; D[1,1] = Dy**2; D[2,2] = Dz**2;
p1 = PyrD_features_df.loc[w, ['PlacementPyr_x', 'PlacementPyr_y', 'PlacementPyr_z'] ].values
p2 = PyrD_features_df.loc[w, ['MinDistCA3_x', 'MinDistCA3_y', 'MinDistCA3_z'] ].values
p3 = PyrD_features_df.loc[w, ['MinDistSub_x', 'MinDistSub_y', 'MinDistSub_z'] ].values
por = PyrD_features_df.loc[w, ['MinDistOriens_x','MinDistOriens_y','MinDistOriens_z'] ].values
plm = PyrD_features_df.loc[w, ['MinDistLacun_x','MinDistLacun_y','MinDistLacun_z'] ].values
# create eigenvectors: semi-axes of the first ellipsoid (vx, vy, vz)
# eigenvector vx : orientation from pyramidal towards subiculum
vx = p3 - p1
vx = vx / np.linalg.norm(vx,2)
# vector vsub : from CA3 towards pyramidal
vsub = p1 - p2
vsub = vsub / np.linalg.norm(vsub,2)
# vector vnorm : normal to (vx , vsub) plane
# vy : ellipses semi-axis
vnorm = np.cross(vx,vsub)
vnorm = vnorm / np.linalg.norm(vnorm,2)
vy = vnorm
# vz : normal to vx and vy
vz = np.cross(vx,vy)
V = np.stack((vx, vy, vz), axis=1)
Q = np.dot(V,np.dot(D,V.T))
(A,V) = np.linalg.eig(Q)
s = np.argsort(A)
D = np.sort(A)
V = V[:,s]; D = np.real(D)
uv = np.arange(-1,1+2/(N-1),2/(N-1))
u,v = np.meshgrid( uv *np.pi/2, uv *np.pi )
# x,y,z for definition of concentric ellipses
x = D[0]**.5 * np.cos(u) * np.cos(v)
y = D[1]**.5 * np.cos(u) * np.sin(v)
z = D[2]**.5 * np.sin(u)
# shift vector to mode ellipsoid so that pyramidal cell placement is inside the ellipsoid
Vshift = 0.85 * Dx * vx
# temporary coordinates of ellipsoid center
qtemp = np.zeros(3)
qtemp[0] = p1[0] + Vshift[0]
qtemp[1] = p1[1] + Vshift[1]
qtemp[2] = p1[2] + Vshift[2]
xx = np.zeros((N,N)); yy = np.zeros((N,N)); zz = np.zeros((N,N));
for k,j in product( range(len(x)), range(len(x)) ):
point = - np.dot( V, np.vstack([x[k,j], y[k,j], z[k,j]]) )
xx[k,j] = point[0] + qtemp[0]
yy[k,j] = point[1] + qtemp[1]
zz[k,j] = point[2] + qtemp[2]
# allocate in (axon1) the coordinates of first axonal cloud
P = np.hstack([ np.reshape(xx,(-1,1)) , np.reshape(yy,(-1,1)) , np.reshape(zz,(-1,1)) ])
P = np.hstack([ P , np.ones((np.size(P,0),1)) * w ])
PyrD_M[w]['AXON'] = P
#### CREATE COORDINATES OF BASAL AND APICAL DENDRITES ####
# u and v are parallel to the axon travelling towards subiculum
u = vx
v = vy
vlm = plm - p1
vlm = vlm / np.linalg.norm(vlm,2)
Dlm = PyrD_features_df['MinDistLacun'][w]
# cone1 is the BASAL one (the upper, shorter and larger, inserted in stratum oriens)
# cone2 is the APICAL one (the lower, longer and narrowe, inserted in stratum radiatum)
H1 = PyrD_features_df['H_BasalDend'][w]
H2 = PyrD_features_df['H_ApicalDend'][w]
Vcone1 = H1 * vlm
Vcone2 = H2 * vlm
O = PyrD_features_df.loc[w, ['PlacementPyr_x','PlacementPyr_y','PlacementPyr_z']].values #cone origin
P1 = np.zeros(3); P2 = np.zeros(3);
P1[0] = O[0] + Vcone1[0] # origin of cone1 circular base
P1[1] = O[1] + Vcone1[1]
P1[2] = O[2] + Vcone1[2]
P2[0] = O[0] - Vcone2[0] # origin of cone2 circular base
P2[1] = O[1] - Vcone2[1]
P2[2] = O[2] - Vcone2[2]
d1 = np.hstack([O[0] - P1[0] , O[1] - P1[1] , O[2] - P1[2] ])
d2 = np.hstack([O[0] - P2[0] , O[1] - P2[1] , O[2] - P2[2] ])
N = 100 # number of points for the description of cross section (volume)
theta = np.random.rand(N,1) * 2 * np.pi
h1 = np.random.rand(N,1) * H1
h2 = np.random.rand(N,1) * H2
R1 = np.random.rand(N,1) * PyrD_features_df['r_BasalDend'][w]
R2 = np.random.rand(N,1) * PyrD_features_df['r_ApicalDend'][w]
x1 = O[0] + (h1/H1)*d1[0] + R1*(h1/H1)*np.cos(theta)*u[0] + R1*(h1/H1)*np.sin(theta)*v[0]
y1 = O[1] + (h1/H1)*d1[1] + R1*(h1/H1)*np.cos(theta)*u[1] + R1*(h1/H1)*np.sin(theta)*v[1]
z1 = O[2] + (h1/H1)*d1[2] + R1*(h1/H1)*np.cos(theta)*u[2] + R1*(h1/H1)*np.sin(theta)*v[2]
x2 = O[0] + (h2/H2)*d2[0] + R2*(h2/H2)*np.cos(theta)*u[0] + R2*(h2/H2)*np.sin(theta)*v[0]
y2 = O[1] + (h2/H2)*d2[1] + R2*(h2/H2)*np.cos(theta)*u[1] + R2*(h2/H2)*np.sin(theta)*v[1]
z2 = O[2] + (h2/H2)*d2[2] + R2*(h2/H2)*np.cos(theta)*u[2] + R2*(h2/H2)*np.sin(theta)*v[2]
# allocate in (dendrite1) and (dendrite2) the coordinates of basal and apical dendrites.
# allocate in (DENDRITES) all the dendrites
Pyrtemp[w] = {}
Pyrtemp[w]['dendrite1'] = np.hstack([ x1 , y1 , z1, np.ones((len(x1),1))*w ])
Pyrtemp[w]['dendrite2'] = np.hstack([ x2 , y2 , z2, np.ones((len(x2),1))*w ])
PyrD_M[w]['DENDRITES'] = np.vstack([ Pyrtemp[w]['dendrite1'] , Pyrtemp[w]['dendrite2'] ])
PyrD_M[w]['dendrite1'] = Pyrtemp[w]['dendrite1']
PyrD_M[w]['dendrite2'] = Pyrtemp[w]['dendrite2']
# convex hull or convex envelope of a shape is the smallest convex set that contains it
PyrD_M[w]['AXONShull'] = ConvexHull( PyrD_M[w]['AXON'][:,0:3] )
pyramidal cell n: 1 pyramidal cell n: 2 pyramidal cell n: 3 pyramidal cell n: 4 pyramidal cell n: 5 pyramidal cell n: 6 pyramidal cell n: 7 pyramidal cell n: 8 pyramidal cell n: 9 pyramidal cell n: 10 pyramidal cell n: 11 pyramidal cell n: 12 pyramidal cell n: 13 pyramidal cell n: 14 pyramidal cell n: 15 pyramidal cell n: 16 pyramidal cell n: 17 pyramidal cell n: 18 pyramidal cell n: 19 pyramidal cell n: 20 pyramidal cell n: 21 pyramidal cell n: 22 pyramidal cell n: 23 pyramidal cell n: 24 pyramidal cell n: 25 pyramidal cell n: 26 pyramidal cell n: 27 pyramidal cell n: 28 pyramidal cell n: 29 pyramidal cell n: 30 pyramidal cell n: 31 pyramidal cell n: 32 pyramidal cell n: 33 pyramidal cell n: 34 pyramidal cell n: 35 pyramidal cell n: 36 pyramidal cell n: 37 pyramidal cell n: 38 pyramidal cell n: 39 pyramidal cell n: 40 pyramidal cell n: 41 pyramidal cell n: 42 pyramidal cell n: 43 pyramidal cell n: 44 pyramidal cell n: 45 pyramidal cell n: 46 pyramidal cell n: 47 pyramidal cell n: 48 pyramidal cell n: 49 pyramidal cell n: 50 pyramidal cell n: 51 pyramidal cell n: 52 pyramidal cell n: 53 pyramidal cell n: 54 pyramidal cell n: 55 pyramidal cell n: 56 pyramidal cell n: 57 pyramidal cell n: 58 pyramidal cell n: 59 pyramidal cell n: 60 pyramidal cell n: 61 pyramidal cell n: 62 pyramidal cell n: 63 pyramidal cell n: 64 pyramidal cell n: 65 pyramidal cell n: 66 pyramidal cell n: 67 pyramidal cell n: 68 pyramidal cell n: 69 pyramidal cell n: 70 pyramidal cell n: 71 pyramidal cell n: 72 pyramidal cell n: 73 pyramidal cell n: 74 pyramidal cell n: 75 pyramidal cell n: 76 pyramidal cell n: 77 pyramidal cell n: 78 pyramidal cell n: 79 pyramidal cell n: 80 pyramidal cell n: 81 pyramidal cell n: 82 pyramidal cell n: 83 pyramidal cell n: 84 pyramidal cell n: 85 pyramidal cell n: 86 pyramidal cell n: 87 pyramidal cell n: 88 pyramidal cell n: 89 pyramidal cell n: 90 pyramidal cell n: 91 pyramidal cell n: 92 pyramidal cell n: 93 pyramidal cell n: 94 pyramidal cell n: 95 pyramidal cell n: 96 pyramidal cell n: 97 pyramidal cell n: 98 pyramidal cell n: 99 pyramidal cell n: 100
%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6,6))
ax = Axes3D(fig)
col = np.round(np.linspace(0,255,rP))
cmap = cm.jet
for w in range(rP):
ptsd = PyrD_M[w]['dendrite1']
ax.scatter(ptsd[:,0], ptsd[:,1], ptsd[:,2], '.', color=[0, .8, 0], s=1.8 )
ptsd2 = PyrD_M[w]['dendrite2']
ax.scatter(ptsd2[:,0], ptsd2[:,1], ptsd2[:,2], '.', color=[0, .2, 1], s=1.8 )
pts = PyrD_M[w]['AXON']
ax.plot(pts[:,0], pts[:,1], pts[:,2], '.', c=[.9, 0, .8] , markersize=2 )
fig.suptitle('Hippocampus (deep) pyramidal cells morphology')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.grid(False)
plt.show()
# deep vs superficial pyramidal cells
%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6,6))
ax = Axes3D(fig)
col = np.round(np.linspace(0,255,rP))
cmap = cm.jet
for w in range(50):
### DEEP (yellow)
ptsd = PyrD_M[w]['DENDRITES']
ax.scatter(ptsd[:,0], ptsd[:,1], ptsd[:,2], '.', color=[.85, .85, 0], s=1.8 )
pts = PyrD_M[w]['AXON']
ax.plot(pts[:,0], pts[:,1], pts[:,2], '.', c=[.85, .85, 0] , markersize=2 )
### SUPERFICIAL (red)
ptsd = PyrS_M[w]['DENDRITES']
ax.scatter(ptsd[:,0], ptsd[:,1], ptsd[:,2], '.', color=[.9, 0, .2], s=2 )
pts = PyrS_M[w]['axon1']
ax.plot(pts[:,0], pts[:,1], pts[:,2], '.', c=[.9, 0, .2] , markersize=2 )
pts2 = PyrS_M[w]['axon2']
ax.plot(pts2[:,0], pts2[:,1], pts2[:,2], '.', c=[.9, 0, .2], markersize=2 )
fig.suptitle('Hippocampus pyramidal cells morphology')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.grid(False)
plt.show()
# plot single pyramidal cell
%matplotlib notebook
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6,6))
ax = Axes3D(fig)
col = np.round(np.linspace(0,255,rP))
cmap = cm.jet
w=3
ptsd = PyrD_M[w]['dendrite1']
ax.scatter(ptsd[:,0], ptsd[:,1], ptsd[:,2], '.', color=[0, .8, 0], s=1.8 )
ptsd2 = PyrD_M[w]['dendrite2']
ax.scatter(ptsd2[:,0], ptsd2[:,1], ptsd2[:,2], '.', color=[0, .2, 1], s=1.8 )
pts = PyrD_M[w]['AXON']
ax.plot(pts[:,0], pts[:,1], pts[:,2], '.', c=[.9, 0, .8] , markersize=3 )
#for simplex in PyrD_M[w]['AXONShull'].simplices:
# ax.plot(pts[simplex,0], pts[simplex,1], pts[simplex,2], '-k', lw=.5)
ax.set_axis_off()
plt.show()
#df = pd.DataFrame(PyrS_M)
#df